niedziela, 10 października 2010

Czas Połowicznego rozpadu

Czas połowicznego rozpadu

Z Wikipedii, wolnej encyklopedii
Skocz do: nawigacji, szukaj
Czas połowicznego rozpadu (zaniku) (okres połowicznego rozpadu) jest to czas, w ciągu którego liczba nietrwałych obiektów lub stanów zmniejsza się o połowę. Czas ten, oznaczany symbolem T1/2, zgodnie z definicją musi spełniać zależność:
N(t)= N_0 \cdot \left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}}
gdzie
N(t) – liczba obiektów pozostałych po czasie t,
N0 – początkowa liczba obiektów.
Pierwotnie czas ten dotyczył nietrwałych jąder atomowych pierwiastków (promieniotwórczych). W tym przypadku po czasie połowicznego rozpadu aktywność promieniotwórcza próbki zmniejsza się również o połowę. Okres połowicznego rozpadu dotyczy również nietrwałych cząstek. Może być wyznaczony z wykładniczego charakteru rozpadu, który w przypadku izotopów promieniotwórczych nosi nazwę prawa rozpadu naturalnego.

Spis treści

[ukryj]

Fizyczny czas połowicznego zaniku [edytuj]

Czas połowicznego zaniku charakteryzuje dany izotop promieniotwórczy niezależnie od czynników zewnętrznych (np. temperatura, ciśnienie, postać chemiczna, stan skupienia itp.). Czas połowicznego zaniku jest pojęciem stosowanym dla każdego rodzaju rozpadu promieniotwórczego.
Czasami ze względów praktycznych i tylko w technice przyjmuje się w przybliżeniu, że całkowity rozpad danego radionuklidu następuje po czasie równym pięciu czasom połowicznego zaniku (tj., gdy aktywność spadnie do poziomu 1/32 aktywności początkowej).
Wszystkie rozpady w przyrodzie można opisać za pomocą trzech powiązanych ze sobą parametrów:
λ – stała rozpadu promieniotwórczego (określa prawdopodobieństwo zajścia rozpadu jednego jądra w jednostce czasu),
T1/2 – okres połowicznego zaniku,
τ – średni czas życia (czas, po którym średnio pozostaje 1/e początkowej liczby cząstek).
Przypuśćmy, że początkowo jest N0 cząstek nietrwałych, po czasie t ich ilość zmniejsza się do N(t).
Prawdopodobieństwo przeżycia przez cząstkę czasu t jest opisywane przez funkcję postaci
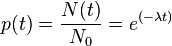p(t)=\frac{N(t)}{N_0}=e ^{(-\lambda t)}.
W związku z tym prawdopodobieństwo p(t) = 1/2, odpowiada czasowi
t = T_{1/2} = \frac{\ln 2}{\lambda}
Średni czas życia oblicza się ze wzoru
\tau = \langle t \rangle = \frac{\int\limits ^{\infty} _{0} t e ^{-\lambda t} dt}{\int\limits ^{\infty} _{0} e ^{-\lambda t} dt} = \frac{-1/\lambda ^{2}}{-1/\lambda} = \frac{1}{\lambda}